Alan wrote a good backgrounder to Metcalfe’s law: “A Short discussion on Metcalfe’s Law for Social Networks.” If you haven’t come across Metcalfe’s Law before, here is the basic background. When Metcalfe (of Ethernet and 3Com fame) started playing with computer networks, he saw that the value of the network was related to the number of devices (nodes) on it, but with exponential returns as you added more devices. There is a lot to be learnt from information theory and network theory that can be applied to social computing, and even to how we manage our personal network of contacts and friends.

At the time, networks were new and exciting things – they were the web 2.0 of their time. Ethernet, Bob Metcalfe’s technology, had some unusual properties, which are still true nearly 30 years on, now that it connects almost every computer in the average office:

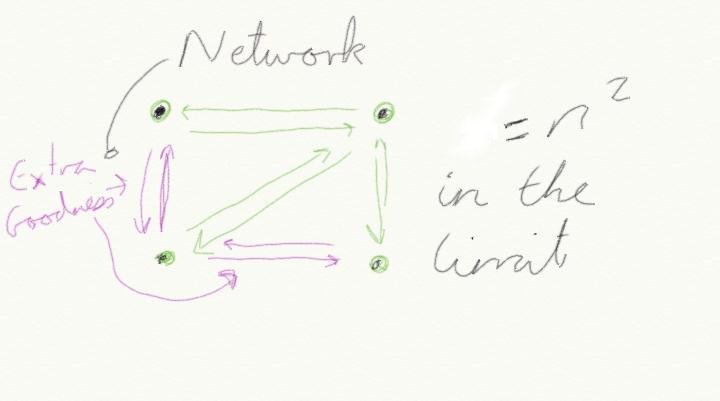
  • Everything ON an Ethernet network is connected TO everything on the network (hold that thought).
  • All connections are equal, in as much as it didn’t matter where you connected, you got the same.
  • Everything on the network receives everything sent to the network (this one has changed slightly).

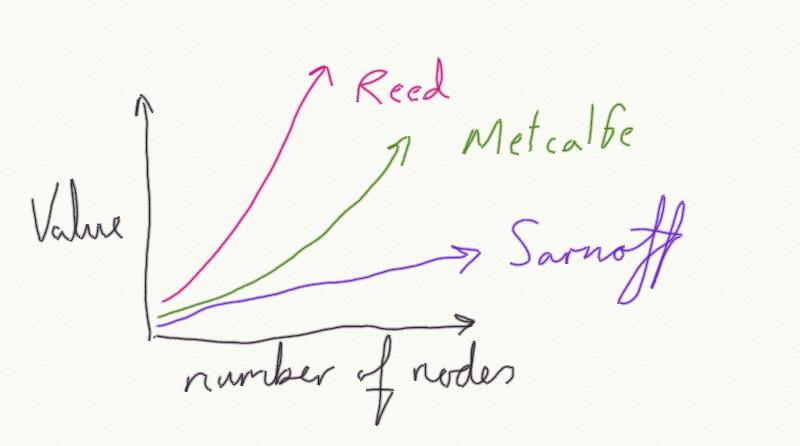
Compared to point to point or ring based networks most of us fought with at the time, this was revolutionary stuff. Metcalfe asserted that the value of such a network was the square of the number of nodes on it: n^2 (or n x n for the benefit of Windows calculator in basic mode). A picture explains better:

Diag 1

Matcalfe’s law

Matcalfe’s law has been held up along side the likes of Moore’s Law as the foundation of Internet growth, but there are at least a couple of problems with that:

  • A. It was never really an empirically proven law.
  • B. If it was, we have well and truly broken it.

Alan points to some of the reasons for that, but I’d like to dissect it another way, in thinking about social networks and social media. There are some implicit assumptions in Metcale’s law:

  1. All nodes start equal (a node here could be a computer, person, etc…).
  2. Every node is equally connected.
  3. The interaction of the nodes does not change their value (all nodes stay equal).

If these three things aren’t true for today’s Internet or for social networks, then Metcalfe’s Law probably does not apply. Are they true? Do they reflect a network with people as nodes? One by one:

  1. In today’s Internet, as with many things, it turns out that not all nodes are equal. In fact it is often an inverse power law, or a 1/n rule. You see this with blogs, where a small proportion account for the majority of traffic. On most computer networks you have desktop machines (clients) and servers. In people you have introverts and extroverts. Definitely not all equal.
  2. The bandwidth or connectivity between nodes is not just about how much is available, it is also about how much is used. We may be able to phone each other, but do we? Also, today’s networks, social or otherwise, have nodes that are connected to more than others – be it Scoble or a Google server. This is the most asymmetric part of social networks and the Internet today.
  3. Transactional models have made a huge difference in Psychology. They apply equally well to social computing. The way that nodes (or people!) interact with each other changes their value, and how they interact with other nodes. I start commenting on a blog, I change its value to others. This interaction is one of the very dynamic things in the blogosphere. A complex dynamic, but a key to the value.

A Different Law of Social Media Networks?

By the way, I’m not throwing stones at the law, that would be far too fashionable, as a quick search would show! Two related laws, which Alan picked up on are Sarnoff’s Law (for broadcast networks – their value is proportional to the number of viewers, nice straight line stuff) and Reed’s Law (which is highly exponential, essential saying that Metcalfe’s law understates the value of a network). Somewhere inbetween Sarnoff’s Law and Reed’s Law is the value of a network. Remember, all of these Law’s say that the value is proportional, we aren’t talking absolutes – we can’t say your network is worth “12” – whatever the units for such a measurement might be.

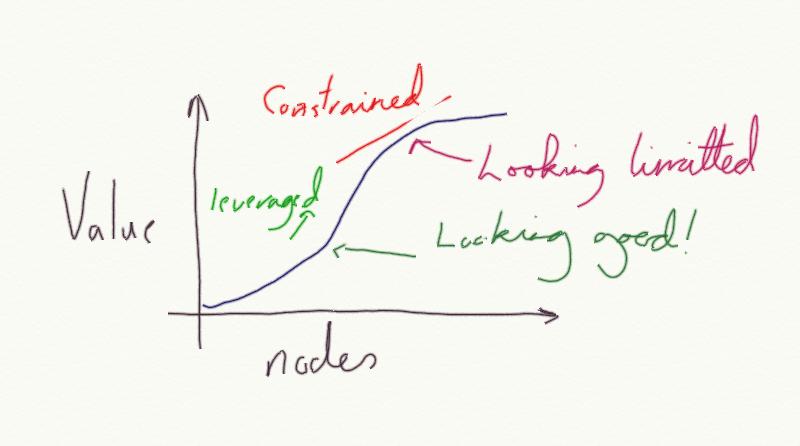
It was the thinking around uncapped exponential models which caused much of the dot com madness – the myth of infinite scale and near infinite value from huge scale. The reality is that networks actually reach a point of diminishing returns. Some have argued for an inverse of Metcalfe’s law for social sites. It is interesting to think about why this is, at least from looking at computer networks:

  • Broadcast noise – this is the reason really big (Ethernet) networks don’t work well. Broadcast packets which go out to everyone, if you get too many devices on the network, sending too many, you end up spending your whole time trying to take it all in. Nodes have no processing power left to get processing done or to send data. This is probably familiar to Twitter addicts! For broadcast media to be two way requires ‘turn taking’ and that gets harder as there are more involved.
  • Finite (global) bandwidth. Bandwidth is finite, based on technology and physical infrastructure (if you want to argue this one, go and look at how many under sea cables there are/aren’t). As you add more devices, they share than bandwidth pool, however it is constrained. That means less and less information can be sent. Think of it this way, what happens if you open 100 web pages at once, or if you had 4,000 friends and a single phone was your only means of communication.
  • Networks in networks. The Internet provides universal connectivity – pretty much everything is connected to pretty much everything, give or take the occasional blip and governmental intervention. However, the network we experience is not the servers and routers that make it up, it is the applications on them. Web servers running blog software and other applications. These are not universally connected. At the high layers, we revert to point-to-point communication, which puts everything back to a linear model. When the conversation moves from the blog to IM or the phone, others loose out, but at scale that is how it has to be.

Metcalfe’s Law and Dunbar’s Number

This all brings me to Dunbar’s Number, which Alan just had to drag into it! For background see earlier posts on the complete bounds of our social networks: Part I and Part II. Many tout the Dunbar number. I it might be better off throwing around Metcalfe. The law was valid at the time, and in the context, but the way that networks work have changed and evolved means that Metcalfe’s law needs to be evolved accordingly, and many a postgrad is pursuing that one. Likewise with the Dundar number.

Dunbar took research on primates, then scaled the numbers to reflect our larger brains. However, we no longer interact as apes do. Our day to day communication is not just face to face, but increasingly mediated by technology. Ambient communication (like Twitter), blogs, photosharing, Dopplr and Instant Messaging are changing the nature of our communications and relationships.

Welcome to the global beta program, there is no planned release date, little support, no product manager and no uninstall option. We need to take the best that we know, from psychology, systems theory and wherever else we can find, and hold on tight for the ride!